Simulons des pandémies

Simulation de pandémies et évaluation basique des mesures de restriction

Cet article a pour but de transmettre un retour d’expérience sur la simulation de pandémies. Objectif? Comprendre les limites et l’intérêt de ces algorithmes. (Et si vous aussi vous souhaitez jouer, le code est libre!)

Quel type de simulation choisir?

Je divise personnellement les simulations de pandémies en deux sortes. Les simulations “statistiques” et les simulations “physiques”. Pour davantage de détail sur les différents types existants, voir ici et là.

Les premières se basent essentiellement sur des statistiques existantes. Ainsi, si un pays dénombre 1000 cas/jour pendant une semaine, il existe un intervalle crédible de cas pour la deuxième semaine, la troisième etc... Cet intervalle peut s’estimer à partir de l’évolution dans le temps du nombre de cas lors des semaines passées dans ce pays ou dans d’autres pays. Ces simulations sont très utiles pour avoir une première idée de la situation future sur un temps court mais elles permettent difficilement une analyse fine de différents scénarios qui n’auraient jamais été testés dans des pays suffisamment similaires.

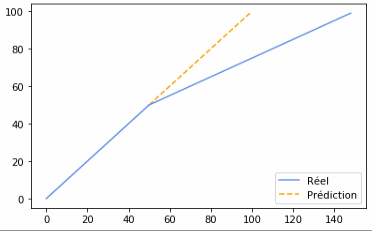
Exemple: https://science.sciencemag.org/content/sci/369/6

Les secondes, les simulations “physiques”, visent à reproduire avec exactitude les phénomènes sociaux en jeu au plus faible niveau d’aléa statistique. Ce sont des systèmes multi-agent. Ainsi, même si ces simulations doivent encore reproduire l’aléatoire fondamental de la contamination et des déplacements d’individus, elles permettent d’extrapoler, sans forcément une connaissance préalable en population générale, les résultats d’une politique sanitaire.

Exemple: un virus se transmet par l’air, les masques peuvent bloquer le virus partiellement. Admettons qu’une première étude abaisse de 90% à 20% le risque de transmission entre deux individus masqués à 1 mètre l’un de l’autre ensembles pendant 2h et que le masque est correctement porté 6h par jour.

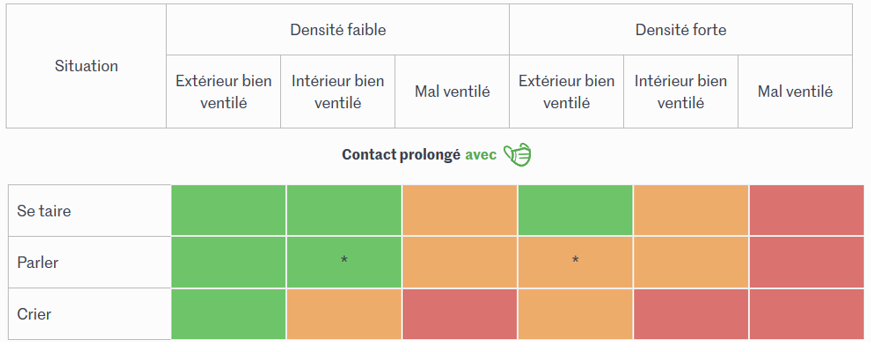
Ces chiffres ont un intérêt, mais ne sont pas utilisables sur une simulation “statistique”. Est-ce que cela réduit les contaminations totales de 10%? 50%? 90%? Il est difficile d’avoir un avis définitif sans savoir si les individus déjà contaminés portaient un masque ou non, sans savoir la fréquence des contacts entre individus etc.

L’intérêt d’une simulation physique est qu’elle va permettre de directement modéliser des situations permettant d’utiliser les pourcentages de base des contaminations, tout en mesurant l’impact au niveau global. Je vais pouvoir mettre “porter un masque réduit de 60% les chances qu’a un individu d’en contaminer un autre” et regarder l’impact sur les courbes épidémiques.

Exemple: https://www.nature.com/articles/s41591-020-1001-6

Nous allons donc nous intéresser aux simulations physiques.

La mise en pratique et le code

Toutes les simulations ont un niveau de finesse établi ainsi que des hypothèses de départ. Ainsi, même s’il serait plus pertinent de modéliser l’ensemble de la population mondiale au centimètre près dans ses interactions à la seconde près, les puissances de calculs de nos ordinateurs ne permettent pas encore cela.

Une simulation physique c’est donc avant tout une liste de choix, de simplifications, et ces choix conditionnent fondamentalement les résultats obtenus. Avant de présenter des résultats, il faut donc présenter des choix, dans notre cas:

• La modélisation avance d’une heure par itération
• Une probabilité par heure et par distance entre deux individus détermine la contamination
• Les individus bougent aléatoirement de quelques mètres par heure sauf à certaines heures

Ces choix sont structurants de la simulation, ils déterminent le phénomène observé. D’autres choix sont flexibles, ils sont déterminés par des variables et influencent les résultats de la simulation: nombre d’individus par population, nombre de populations, amplitude des échanges entre les populations, taux d’individus confinés/immobiles, heures de sommeil, présence d’un couvre feu immobilisant plus tôt, probabilité de décès par heure d’un individu contaminé, durée de la contamination, délai avant capacité à infecter, densité de la population, durée d’infection avant possibilité de décès, proportion initiale de contaminés etc.

Tous ces choix déterminent également le déroulé de la simulation. Ainsi, dans ma simulation, les individus n’ont pas de “chez eux”, ils ne font pas la fête, ils n’ont pas de travail et ils ne prennent pas les transports en commun. Ils vivent tous dans un plus ou moins grand gymnase et ne font que errer aléatoirement à l’intérieur en dormant sur le sol, sans manger. Comme une prison à zombie. Selon la proximité qu’on attache entre ma simulation de prisons à zombie et la vie réelle, on accordera plus ou moins d’importance à ces résultats.

Le code de simulation (python) peut être retrouvé ici: https://github.com/Whiax/SimulationPandemie

Le code principal dans simulation.py tient en 300 lignes.

Un exemple de paramètre chiffré qui ne change pas au cours des simulations: chaque heure, un individu présent à 10cm d’un individu contaminant a 95% de chances d’être contaminé, à 50cm c’est 90%, à 1m c’est 70%, à 2m c’est 60% et de 2m à 5m c’est 30%.

Une référence bibliographique peut être celle-ci: 9 contaminés sur 31 dans un rayon de 4.5m en 30 minutes. Pour 30% de contaminés toutes les 30 min, nous avons 50% de contaminés toutes les heures.

Autre référence: 10 contaminés sur 31 personnes dans un espace de dimension 5m² pendant 1h. 32% de contaminés par heure.

Les résultats

1) La simulation dense - 1 population, 1000 individus, 16 m² / individu

Voici un exemple de propagation d’un virus dans une simulation de 1000 individus qui ne dorment pas:

En rouge, un malade. En bleu, un individu sain. En vert, un individu guéri et immunisé; en noir un individu décédé (il ne bouge pas, c’est l’échelle du graphique qui bouge).

Dans cette simulation, après 2 mois, 88.7% des individus ont été infectés ce qui conduit de fait à une immunité de masse, le virus n’arrive plus à circuler car les derniers individus infectés ne rencontrent plus que d’autres individus immunisés. Sans compter que les individus restants à infecter sont plus éloignés des zones denses.

On remarque notamment, à travers la zone rouge puis verte centrale, que les individus les plus épargnés sont ceux qui arrivent à s’éloigner des zones les plus denses juste avant le pic épidémique. La densité initiale de cette simulation était de 16 m²/individu, tentons avec une densité de 24 m²/individu.

2) Des simulations moins denses - 24 m² / individu

Les visuels sont jolis mais apporte peu d’informations sur les tendances. Rajoutons à cela une étude statistique, voici les courbes de contaminations à 1 individu tous les 24 m².

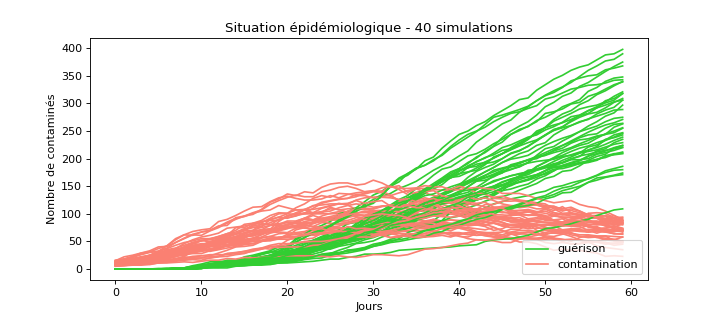
Attention les courbes “rouges” ne comptent pas les nouvelles contaminations, chiffre habituellement rapporté, mais bien le nombre total de contaminés simultanément dans la population. Un individu reste contaminé 2 semaines. Je n’affiche pas les décès car dans une population de 1000 individus avec 0.6% de chances de décès, le chiffre final est assez dérisoire.

On voit que dans ces simulations moins denses, sur la même durée, le nombre de contaminé total est nettement plus faible avec une moyenne à 25% en comparaison des 88.7% de la simulation précédentes.

Les courbes sont assez aléatoires, en réalité avec d’autres hypothèses de départ certains scénarios se finissent même en 15 jours sans aucune contamination secondaire, d’autres ont un pic à 30 jours, et d’autres à 15. On peut donc parfaitement imaginer l’hypothèse du porteur du virus qui arrive dans une population vulnérable sans créer de vague épidémique.

En revanche, une fois une vague démarrée, et sans changement d’hypothèse, il semble que seule une immunité de masse des individus dans les zones denses permette la fin de l’épidémie.

3) La densité initiale comme paramètre

Faisons varier la densité initiale et analysons le résultat sur les courbes de contaminés:

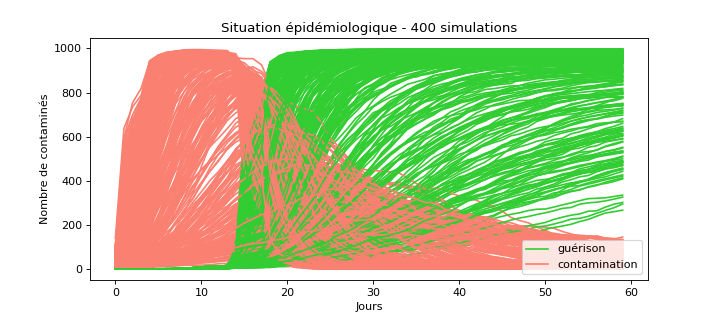
... analysons le résultat sur les courbes MOYENNES de contaminés:

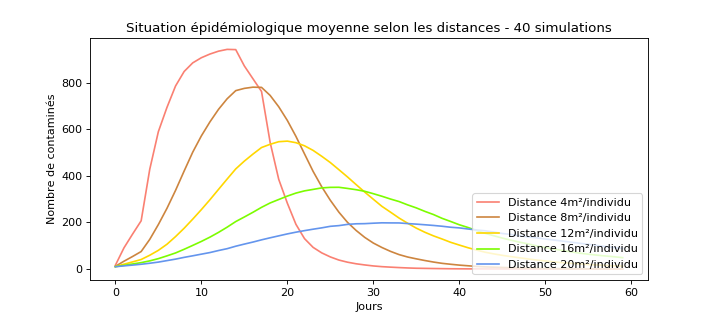
Sans surprise, ajouter de la distance entre les individus permet de drastiquement freiner les contaminations.

On remarque également que réduire l’amplitude du pic épidémique se traduit également par un allongement de la durée précédant le pic épidémique.

Une éventuelle limite est la non prise en compte d’une trace que laisserait les individus malades dans leur sillage: poignée de porte, objets touchés, virus en aérosol etc.. Cependant ce genre de détail peut fonctionnellement être ajouté à la simulation sans trop de difficultés. La difficulté est d’estimer le risque infectieux laissé par cette trace, mais la durée de vie du virus en aérosol ou sur des matériaux est quantifiée.

4) Pierre va chez Paul: 4 populations, 1000 individus, 16m² / personne

Intéressons-nous à présent aux échanges de population. Ces simulations s’ancrent dans la question de la fermeture des frontières (quelque soit le niveau: municipal, départemental, régional, national ou international), questions très débattues en France depuis Mars: ici, ici, là, ici, là etc.

“Le virus est déjà là. Ça n’aurait même pas de sens, […]”

— Pascal Crépey, épidémiologiste, Juillet

ou

“Une réponse qui scientifiquement n’a pas d’intérêt”

— Olivier Véran, Ministre de la Santé, Mars

Vérifions cela en comparant plusieurs situations. Dans la première, les frontières sont fermées. Dans les autres elles sont ouvertes: nous avons un échange aléatoire à x% de chances de transférer y% individus qui, toutes les heures, vont rejoindre un autre individu dans une autre population (téléportation sur un endroit occupé puis errance). Evidemment les individus transferrés peuvent être sains ou malades.

Données de la simulation: 16m² par individu (courbe jaune sur le schéma au dessus), 4 populations de 1000 individus. Je lance 80 simulations par scénario et j’observe la médiane des contaminations totales, par jour, entre les situations.

Les probabilités horaires de transfert sont de 0/0.01/0.02/0.05/0.1. Le taux de population transféré est équivalent à la probabilité de transfert, à 0.05 on transfère donc 5% de la population avec 5% de chance par heure.

Comparons avec un chiffre réel: Les trois quarts des actifs franciliens changent de commune pour aller travailler. Nous avons donc un déplacement équivalent de 75% de la population le matin et de 75% le soir, soit 150% par jour soit 100% de chance d’échanger 9.4% de la population par heure “éveillée”. Ici le scénario avec le plus de transfert est à 10% de chance d’échanger 10% de la population par heure “éveillée” (donc en moyenne 16% par jour au total contre 150% dans la réalité):

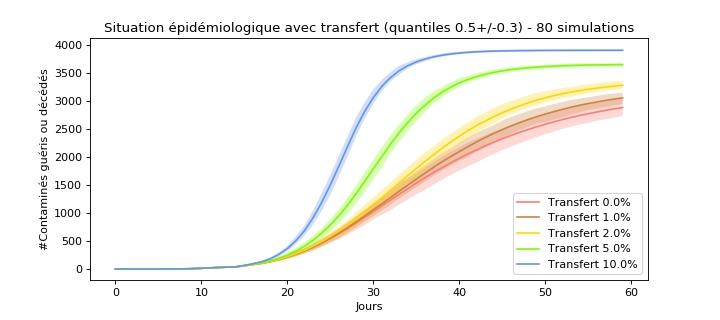
Il est important de comprendre que les différentes populations ont une situation identique en tendance au début de l’épidémie. Donc à situations initiales identiques, le transfert de population amplifie la pandémie.

Comment cela s’explique-t-il? Et bien une hypothèse est que les individus malades venant d’une population largement contaminée participe à la contamination des individus sains dans une population moins contaminée, cela en comprenant que les situations peuvent être identiques initialement (quoique jamais réellement), mais elles peuvent aussi réellement diverger par la suite. Le transfert de population limite cette divergence et uniformise les situations des populations. Mais cette uniformisation se fait dans le sens du pire.

Nous pouvons également ajouter l’hypothèse que les transferts de populations se font de façon plus soutenue entre les zones plus denses et donc plus touchées ou plus touchables, cette simulation reproduit ce phénomène puisqu’elle transfère un individu aléatoirement sur la position d’un autre dans une autre population, et ces autres individus sont davantage présents dans les zones plus denses.

La réponse de limitation des transferts de population, selon les hypothèses de départ, a donc un intérêt, quelque soit l’échelle géographique choisie.

5) Quel impact pour un “couvre feu”?

Ici un couvre feu se traduit par une interdiction de mouvement plus tôt dans la journée. Les individus bougent sauf de minuit à 8h. Avec un couvre feu, les individus bougent sauf de 21h (ou autre) à 8h.

Nous gardons une population par simulation, seul le couvre-feu change.

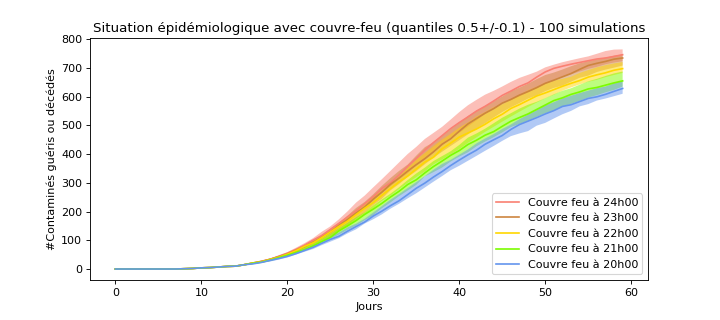
On remarque une relation dose-effet, plus le couvre feu se fait tôt, meilleure est la situation épidémique finale, avec une réduction de ~10% en passant l’heure de repos de minuit à 20h. Cela équivaut environ au passage de 16m² par individu à 18m² par individu.

Cette réduction de 10% peut néanmoins être considérée comme faible compte-tenu de l’impact d’un couvre-feu à 20h.

Cela dit cette simulation simpliste ne modélise pas une éventuelle différence d’exposition au virus en fonction de l’heure ou des activités. Ces éléments peuvent être observés dans des analyses statistiques empiriques et conduire à donner une importance plus grande au couvre-feu.

6) Quel impact pour un “confinement”?

Passons au confinement et testons plusieurs scénarios. Lors d’un confinement, la population n’est jamais confinée à 100%. Dans cette simulation, un confinement signifie une incapacité de mouvement de X% de la population sur 24H.

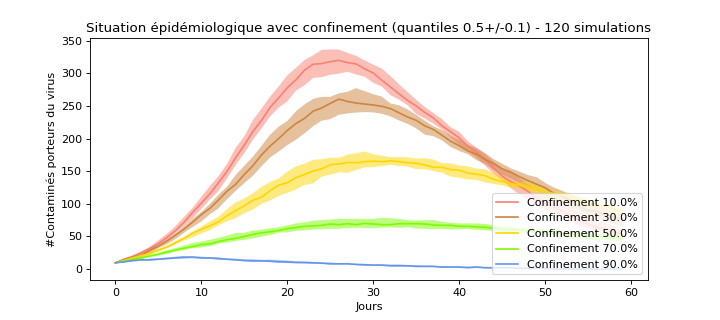
A contrario d’un couvre-feu qui semble être une mesure assez légère dans la simulation, un confinement est une mesure qui, si elle est forte, permet de nettement réduire l’amplitude du pic épidémique.

Le confinement tel qu’il est mis en place dans la réalité doit également être vu comme une mesure d’arrêt des transferts entre populations puisque les déplacements d’une population vers une autre sont également supprimés ou diminués. On voit que plus l’amplitude du confinement est élevée, plus il y a une certitude de son efficacité. A 90% de confinement, seuls 10% des individus de la population sont habilités à bouger tous les jours, l’épidémie se termine en une trentaine de jours.

C’est fini pour les résultats, d’autres scénarios peuvent être testés et fournis à la demande ou en utilisant le code. On peut imaginer tester des taux d’immunité initiaux dans le cas d’un vaccin ou d’une seconde/troisième vague, ajouter des seuils épidémiques en fonction des capacités des hôpitaux etc.

Conclusion

Nous avons pu observer dans les simulations l’impact de certaines métriques sur le déroulé d’une épidémie simulée. Ces simulations, quand elles sont à un niveau cohérent de réalisme, permettent d’anticiper l’impact d’une mesure politique sur le déroulé épidémique. Même quand elles ont un niveau peu élevé de réalisme, elles permettent de se faire un premier avis sur l’émergence de phénomènes globaux à partir de la modélisation de phénomènes locaux.

Intérêts

• Ce qu’on apprend sur les transferts entre populations: Ces simulations montrent que les mesures de restrictions d’échanges d’individus entre populations sont des mesures qui, aux limites des simulations près, ont une base scientifique cohérente.
• Anticipation des politiques sanitaires: Dans un cadre suffisamment réaliste, l’utilisation de ces simulations permettrait de guider finement les décisions prises par les autorités au niveau le plus local possible en fonction des comportements observés, de la densité des lieux, de la topologie des territoires et d’autres paramètres sociaux et géographiques. Vaut-il mieux confiner des villes ou obliger le port correct du masque en permanence? Limiter les transferts de populations? Astreindre une distanciation sociale? Quel taux de vaccination faut-il atteindre? Quelles populations faut-il cibler? Les simulations physiques réalistes peuvent apporter des réponses à ces questions.
• Anticipation des conséquences économiques: Ces simulations n’ont pas vocation à s’arrêter aux conséquences sanitaires, ainsi autant qu’un confinement a des conséquences épidémiques pouvant être modélisées, il a des conséquences économiques qui peuvent être anticipées. La simulation parfaite minimiserait le risque économico-sanitaire conjointement. “Fournis moi les mesures sanitaires garantissant un arrêt de l’épidémie et minimisant le coût économique” : Voilà un énoncé réalisable dans le cadre d’une simulation physique. Une simulation pourrait même fournir une dizaine de scénarios différents, à charge des responsables de choisir le plus toléré socialement.
• Vérification des connaissances existantes: Les modèles se basent sur des éléments statistiques. Si un modèle cohérent ne prédit pas un comportement observé, c’est donc qu’il y a un phénomène réel qui n’est pas compris. Les courbes épidémiologiques correspondent-elles à une transmission majoritairement manuportée? A une transmission par aérosol? Les simulations permettent de fournir des réponses à ces questions.
• Pédagogie: Ces simulations peuvent également être intéressantes dans un but pédagogique. Ainsi, se baser sur les résultats d’une simulation peut permettre de justifier les mesures politiques prises ou de faire comprendre leur efficacité potentielle à la population. Avoir un code de simulation ouvert et financer les individus qui y participent permettrait également d’avoir une amélioration perpétuelle de son réalisme et de ses résultats, tout en ayant des citoyens impliqués dans la modélisation et la compréhension des simulations aboutissant à une prise de décision.

Limites

• Le réalisme: Plus il y a un investissement dans ces projets, autant humain que matériel, plus le réalisme peut être augmenté. L’investissement humain est fondamental car c’est un travail minutieux que de modéliser de façon réaliste les allers retours journaliers de millions d’individus tout comme leur risque de recevoir et de transmettre un virus. L’objectif est évidemment de sortir de l’effet “prison à zombie” en étant capable de créer de fins réseaux sociaux comme il en existe dans la réalité, ajouter l’âge des individus, leur risque tel que vérifié par les données empiriques etc. D’un côté il faut modéliser des phénomènes locaux réels, et de l’autre les faire correspondre aux résultats empiriques.
• Les optimisations: L’aspect matériel est en réalité probablement secondaire. Des algorithmes tels que quadtree permettent d’optimiser ces calculs et on peut également imaginer mettre à profit le calcul parallèle sur GPU afin d’effectuer des simulations mettant en jeu des millions d’individus. Et même sans cela, on peut imaginer extrapoler une bonne mesure sur 100.000 individus à 10 millions d’individus, pourvu que la densité et que les échanges soient mis à l’échelle. En sachant également qu’une population de 1 million d’individus correspond à 1000 populations de 1000 individus ayant un certain niveau d’échange entre elles.
• Moyens matériels: L’algorithme fonctionne à 1 simulation de 1000 personnes sur 1 thread CPU à 3.5Ghz en 30secondes, donc environ 60 simulations à la minute sur 16 coeurs — 32 threads
• Moyens humains: 1 Bac+5 pendant 5 jours (analyse et article compris)

Dans cet article, nous avons vu les qualités et les limites des simulations “physiques”. Ces simulations peuvent probablement trouver une place fondamentale dans un modèle de santé moderne de long terme et dans une politique d’anticipation des risques épidémiologiques.

Il parait important de s’inspirer de modélisations physiques avancées existantes dans le but d’orienter les futures politiques sanitaires ou même économiques, d’une façon similaire à ce qui est déjà fait sur l’anticipation des conséquences du dérèglement climatique.

Situation en France de Septembre à Octobre 2020:

____________________________________________

Cet article a été écrit sur Medium, par Elie D, pour https://www.hyugen.com/fr.

Support us 💙

You can follow us on Twitter to show support and to see all news (no tweet-spam, only news), or here on Medium.

Date: 2020/10/22